Before directly jumping to learn the quick sort in the C algorithm, a general question that might come to your mind is, "What is sorting, and why do you need to learn it?" The answer to the question is simple. If you are a software developer , then it becomes necessary that you have the knowledge of all those techniques that are required for software development. Also, sorting is required to reduce the data search time and arrange a large set of data in an organized way to make it useful and more effective. Quick sort is one of the many types of sorting algorithms.
Quick Sort in C
Before seeing the implementation of quick sort in C, let’s first understand the basics of quick sort.
What is Quick Sort?
Quick sort is a highly efficient sorting algorithm. Like merge sort , this algorithm is also based on the divide and conquer technique and uses the comparison method. Quick sort is an ideal solution for a large set of data. The sorting algorithm first divides the array into two sub-arrays by comparing all elements with a specified value, called the Pivot value. The two sub-arrays are divided in a way that one of them holds smaller values than the pivot value, and the other holds greater values than the pivot value. There are different ways to implement quick sort:
- Always pick the last element as a pivot (we'll use this in our quick sort in C example).
- Always pick the first element as the pivot.
- Pick median as the pivot.
- Pick a random element as the pivot.
After the partition, quick sort calls itself recursively to sort the sub-arrays. Quick sort has the time complexity of O(n^2) in the worst and average cases, where n is the number of elements. Therefore, quick sort is quite efficient for large data. The best case is when the pivot element will be the middle element. The best-case time complexity for quick sort is O(n logn). Here is an example of quick sort to understand the sorting technique more easily:
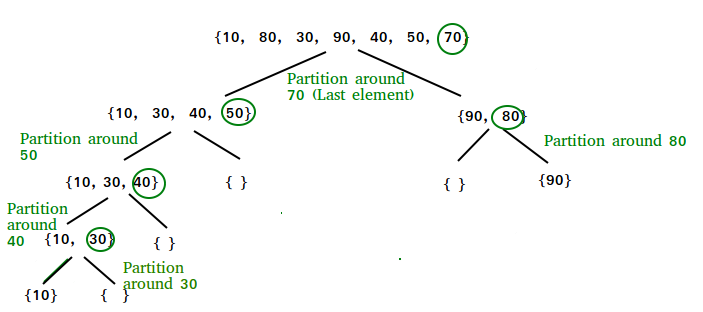
This list contains seven elements. The last element, 70, is the pivot value. Now the list will be partitioned w.r.t. 70 until we get the pivot for each sub-lists and all lists have a single element only.
Steps for the Quick Sort in C Algorithm
- First Step – Start choosing with the highest index value called a pivot.
- Second Step ? Take two variables that indicate the left and right of the list, excluding the pivot value.
- Third Step ? Left variable will show the low index.
- Fourth Step ? Right will point to the high index.
- Fifth Step – If the value at the left index is less than the pivot, then move right.
- Sixth Step ? If the value at the right index is greater than the pivot, then move left.
- Seventh Step ? If both step 5 and step 6 do not match, then swap left and right indexes.
- Eighth Step ? If left ? right, the point where they meet will be the new pivot value.
Quick Sort in C Example
/* QuickSort implementation using C*/
#include<stdio.h>
// Function to swap two elements
void swap(int* a, int* b)
{
int t = *a;
*a = *b;
*b = t;
}
/* This function takes the last element as pivot, places the pivot element at its correct position in a sorted array, and places all smaller than pivot
to the left of the pivot and all greater elements to the right of the pivot. */
int partition (int arr[], int low, int high)
{
int pivot = arr[high]; // pivot
int i = (low - 1); // Index of smaller element
for (int j = low; j <= high- 1; j++)
{
// If current element is smaller than or
// equal to pivot
if (arr[j] <= pivot)
{
i++; // increment index of smaller element
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
/* The main function to implement QuickSort.
arr[] --> Array that is to be sorted,
low --> to show Starting index,
high --> to show Ending index */
void quickSort(int arr[], int low, int high)
{
if (low < high)
{
/* pi is partitioning index, arr[p] is now at right place */
int pi = partition(arr, low, high);
// Separately sort elements before
// partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
/* Function to print an array */
void printArray(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
printf("n");
}
// Driver program to test above functions
int main()
{
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof(arr)/sizeof(arr[0]);
quickSort(arr, 0, n-1);
printf("Sorted array: n");
printArray(arr, n);
return 0;
}
Output:
Sorted array: 1 5 7 8 9 10
Quick Sort in Java Example
// Implementation of QuickSort using Java program
class QuickSort
{
/* This function takes the last element as pivot, places the pivot element at its correct position in the sorted array, and places all smaller (smaller than pivot) to the left of the pivot and all greater elements to the right of the pivot */
int partition(int arr[], int low, int high)
{
int pivot = arr[high];
int i = (low-1); // index of smaller element
for (int j=low; j<high; j++)
{
// If current element is smaller than or
// equal to pivot
if (arr[j] <= pivot)
{
i++;
// swap arr[i] and arr[j]
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// swap arr[i+1] and arr[high] (or pivot)
int temp = arr[i+1];
arr[i+1] = arr[high];
arr[high] = temp;
return i+1;
}
/* The main function that implements QuickSort()
arr[] --> Array to be sorted,
low --> Starting index,
high --> Ending index */
void sort(int arr[], int low, int high)
{
if (low < high)
{
/* pi is partitioning index, arr[pi] is
now at right place */
int pi = partition(arr, low, high);
// Recursively sort elements before
// partition and after partition
sort(arr, low, pi-1);
sort(arr, pi+1, high);
}
}
/* A utility function to print array of size n */
static void printArray(int arr[])
{
int n = arr.length;
for (int i=0; i<n; ++i)
System.out.print(arr[i]+" ");
System.out.println();
}
// Driver program
public static void main(String args[])
{
int arr[] = {20, 17, 3, 9, 2, 5};
int n = arr.length;
QuickSort ob = new QuickSort();
ob.sort(arr, 0, n-1);
System.out.println("sorted array");
printArray(arr);
}
}
Output:
Sorted array: 2 3 5 9 17 20
Quick Sort in C++ Example
#include <bits/stdc++.h>
using namespace std;
void swap(int* a, int* b)
{
int t = *a;
*a = *b;
*b = t;
}
int partition (int arr[], int low, int high)
{
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j <= high - 1; j++)
{
if (arr[j] < pivot)
{
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
void applyQuickSort(int arr[], int low, int high)
{
if (low < high)
{
int pivotIndex = partition(arr, low, high);
applyQuickSort(arr, low, pivotIndex - 1);
applyQuickSort(arr, pivotIndex + 1, high);
}
}
int main()
{
int arr[] = {1, 4, 3, 2, 5};
int n = sizeof(arr) / sizeof(arr[0]);
applyQuickSort(arr, 0, n - 1);
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
return 0;
}
Output
1 2 3 4 5
Quick Sort in Python Example
def partition(start, end, arr): pivotIndex = start pivot = arr[pivotIndex] while start < end: while start < len(arr) and arr[start] <= pivot: start += 1 while arr[end] > pivot: end -= 1 if(start < end): arr[start], arr[end] = arr[end], arr[start] arr[end], arr[pivotIndex] = arr[pivotIndex], arr[end] return end def applyQuickSort(start, end, arr): if (start < end): p = partition(start, end, arr) applyQuickSort(start, p - 1, arr) applyQuickSort(p + 1, end, arr) arr = [ 1, 2, 4, 3, 5 ] applyQuickSort(0, len(arr) - 1, arr) print(arr)
Output
[1, 2, 3, 4, 5]
Advantages of Quick Sort
- The high performance of quick sort makes it immensely popular.
- Quick sort has easy implementation.
- On average, quick sort runs very fast and even faster than the merge sort.
- Quick sort requires no additional memory to hold the variables while sorting.
Disadvantages of Quick Sort
- Quick sort is not stable.
- Running time depends on the size of an array .
- If the pivot selection is unsuccessful, then running time will heavily degrade.
- It is difficult to implement the partitioning and the average efficiency for the worst case.
A Real-Time Application Example of Quick Sort
In real-time problems, whenever you need sorting , you may apply quick sort as it is very efficient. Here is a practical example: Suppose you have a shopping list, and you have a fixed amount of time to purchase the items. You will also be given priorities to decide. Thus, you need to grab the items with the highest priority first. This is the shopping list with items and their priorities: Eggs (4) Bread (2) Milk (6) Meat (1) Detergent (5) Water (3) For small lists, it is easy to arrange the products manually and follow priority numbers. But what about the list of items with a count of 138 or more? What will you do then? Would you check 138 items to find the next item? No, it’s obvious that you don’t have that much time! So you will be reordering the list by priority by taking the first element as a pivot, which is eggs.
STEP 1:
Shift fewer priority elements after eggs and more priority ones before eggs. bread (2) - Group A water (3) - Group A meat (1) - Group A eggs (4) - Pivot milk (6) - Group B detergent (5) - Group B Then repeat the same for each divided group.
STEP 2:
Group A meat (1) bread (2) - Pivot water (3) Group A is done!
STEP 3:
Group B detergent (5) milk (6) - Pivot Group B is done. So what do we have? Group A ordered Pivot (in the place where it needs to be) Group B ordered
STEP 4:
Write them all: meat (1) bread (2) water (3) eggs (4) detergent (5) milk (6) So, for 6 items, you just performed sorting with only 4 steps and got your sorted shopping list by priority.
Conclusion
So that was all about examples of the quick sort in C and other popular programming languages. Like other sorting algorithms, quick sort has its own advantages and disadvantages. So, first, underline your requirements and then choose wisely! People are also reading:
![Quick Sort in C, C++, Java, and Python [Program and Algorithm]](/media/tutorial_images/Quick-Sort-in-C-C-Java-and-Python.jpg)