Maximum size square sub-matrices with all 1's

Problem Statement

Consider a matrix with all 0s and 1s. Your task is to find the largest square sub-matrix, which contains all 1s in it.

Approach 1 - DP (Bottom Up)

This approach is very simple, for every cell in the matrix , consider the cells which surround it.

Example 1 In the below image, consider the left side matrix as arr1[][] and right side matrix as arr2[][].

To find the value of arr2[1][1], we need to find the minimum value of the cells surrounded by it, i.e., arr1[0][0], arr1[0][1], and arr1[1][0]. The value of each cell is as follows: arr1[0][0] = 1, arr1[0][1] = 0, arr1[1][0] = 0 The minimum value is 0. Add 1 with the minimum of these values and write the result in the desired cell. So, arr2[1][1] = 1.

Example 2

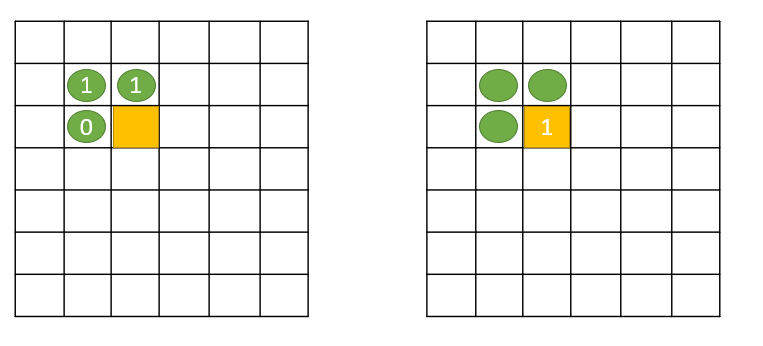
We need to find the value of arr2[2][2], so we find the minimum value of the cells surrounded by it, i.e., arr1[1][1], arr1[1][2], and arr1[2][1]. The values of each cell is: arr1[1][1] = 1, arr1[1][2] = 1, arr1[2][1] = 0 The minimum value is again 0. So, we add the minimum value with 1 and write the result in the desired cell. So, arr2[1][2] = 1.

Example 3

We need to find the value of arr2[1][2], so we find the minimum value of the cells surrounded by it i.e. arr1[0][1], arr1[0][2], and arr1[1][1]. The values are arr1[0][1] = 2, arr1[0][2] = 2, arr1[1][1] = 1. The minimum value is 1 this time. So, we add the minimum value with 1 and write the result in the desired cell. So, arr2[1][2] = 2

Example 4

We need to find the value of arr2[4][6], so we find the minimum value of the cells surrounded by it i.e. arr1[3][4], arr1[3][5], and arr1[4][4]. The values are arr1[3][4] = 2 , arr1[3][5] = 2, and arr1[4][4] = 2. The minimum value is 2.

So, we add the minimum value with 1 and write the result in the desired cell. So, arr2[4][6] = 3. We can follow the same approach mentioned in the above examples to find values for all the cells of a matrix. Following is an input matrix and its resultant matrix: Input matrix:

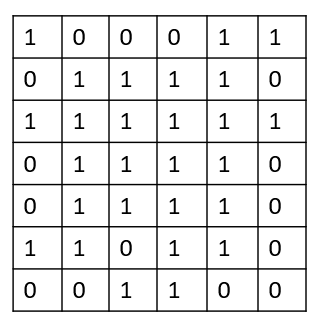
Resultant matrix:

Algorithm:

1. Consider 2 arrays arr1[][] and arr2[][].
2. Copy the given matrix into arr1[][].
3. Now copy the first row and first column of arr1[][] to arr2[][].
4. The below steps must be followed to copy the rest of the matrix:
   • If the value at arr1[][] == 0, simply copy that value to arr2[][] i.e. arr2[][] = 0.
   • If the value at arr1[][] == 1, then arr2[] = min_value(min(arr1[i-1][j-1],arr1[i][j-1],arr1[i-1][j])+1.

We have used Dynamic Programming to solve the above approach.

• C++ Code

#include <bits/stdc++.h>
#define bool int
#define Row 7
#define Column 6
using namespace std;

void MaxSubSquare(bool arr1[Row][Column])
{
	int i,j;
	int arr2[Row][Column];
	int max_arr2, max_of_i, max_of_j;
	
	//Copying first row of arr1 to arr2
	for(j = 0; j < Column; j++)
		arr2[0][j] = arr1[0][j];
		
	//Copying first column of arr1 to arr2
	for(i = 0; i < Row; i++)
		arr2[i][0] = arr1[i][0];
		
	//Other Matrix cells
	i=1;
	while(i<Row)
	{
		j=1;
		while(j<Column)
		{
			if(arr1[i][j] == 1)
				arr2[i][j] = min(arr2[i][j-1],min( arr2[i-1][j],arr2[i-1][j-1])) + 1;
			else
				arr2[i][j] = 0;	
		j++;
		}
	i++;
	}
	
	
	//Finding Maximum entry
	//Finding indexes of maximum entry from arr2
	max_arr2 = arr2[0][0]; max_of_i = 0; max_of_j = 0;
	for(i = 0; i < Row; i++)
	{
		for(j = 0; j < Column; j++)
		{
			if(max_arr2 < arr2[i][j])
			{
				max_arr2 = arr2[i][j];
				max_of_i = i;
				max_of_j = j;
			}
		}			
	}

	cout<<"Possible Maximum Sub Matrix is: \n"; for(i = max_of_i; i > max_of_i - max_arr2; i--)
	{
		for(j = max_of_j; j > max_of_j - max_arr2; j--)
		{
			cout << arr1[i][j] << " ";
		}
		cout << "\n";
	}
}


// Driver code 
int main()
{
	bool arr1[Row][Column] = 	{{1,0,0,0,1,1},
								{0,1,1,1,1,0},
								{1,1,1,1,1,1},
								{0,1,1,1,1,0},
								{0,1,1,1,1,0},
								{1,1,0,1,1,0},
								{0,0,1,1,0,0},
							};
					
	MaxSubSquare(arr1);
}

Output:

• Java Code

public class Main
{
    public static void MaxSubSquare(int arr1[][])
    {
        int i,j;
        int Row = arr1.length;       //no of rows in M[][]
        int Column = arr1[0].length;     //no of columns in M[][]
        int arr2[][] = new int[Row][Column];    
        
        int max_arr2, max_of_i, max_of_j;
    
        //Copying first column to arr2
        for(i = 0; i < Row; i++)
            arr2[i][0] = arr1[i][0];
    
        //Copying first row to arr2
        for(j = 0; j < Column; j++)
            arr2[0][j] = arr1[0][j];
        
        // Other Cells
        for(i = 1; i < Row; i++)
        {
            for(j = 1; j < Column; j++)
            {
                if(arr1[i][j] == 1)
                arr2[i][j] = Math.min(arr2[i][j-1],Math.min(arr2[i-1][j], arr2[i-1][j-1])) + 1;
                else
                    arr2[i][j] = 0;
            }
        }   
        
        //Find Maximum entry
        //Finding indexes of maximum entry from arr2
        max_arr2 = arr2[0][0]; max_of_i = 0; max_of_j = 0;
        for(i = 0; i < Row; i++)
        {
            for(j = 0; j < Column; j++)
            {
                if(max_arr2 < arr2[i][j]) { max_arr2 = arr2[i][j]; max_of_i = i; max_of_j = j; } } } System.out.println("Possible Maximum Sub Matrix is: "); for(i = max_of_i; i > max_of_i - max_arr2; i--)
        {
            for(j = max_of_j; j > max_of_j - max_arr2; j--)
            {
                System.out.print(arr1[i][j] + " ");
            }
            System.out.println();
        }
    }
    
    // Driver program
    public static void main(String[] args)
    {
        int arr1[][] = {{0,1,1,1,1,0},
                                {1,1,1,1,1,1},
                                {0,1,1,1,1,0},
                                {0,1,1,1,1,0},
                                {1,1,0,1,1,0},
                                {0,0,1,1,0,0},};
            
        MaxSubSquare(arr1);
    }
}

Output:

• Python Code

def MaxSubSquare(M):
    R = len(arr1) 
    C = len(arr1[0]) 

    S = [[0 for k in range(C)] for l in range(R)]
    # Copying first row & columnto arr2

    # Other Cells
    for i in range(1, R):
        for j in range(1, C):
            if (arr1[i][j] == 1):
                S[i][j] = min(S[i][j-1],S[i-1][j],S[i-1][j-1])+1
            else:
                S[i][j] = 0
    
    # Find the maximum entry and indices
    max_of_s = S[0][0]
    max_i = 0
    max_j = 0
    for i in range(R):
        for j in range(C):
            if (max_of_s < S[i][j]):
                max_of_s = S[i][j]
                max_i = i
                max_j = j

    print("Maximum size sub-matrix is: ")
    for i in range(max_i, max_i - max_of_s, -1):
        for j in range(max_j, max_j - max_of_s, -1):
            print (arr1[i][j], end = " ")
        print("")

# Driver Program
arr1 = [[0, 1, 1, 0, 1],
    [1, 1, 0, 1, 0],
    [0, 1, 1, 1, 0],
    [1, 1, 1, 1, 0],
    [1, 1, 1, 1, 1],
    [0, 0, 0, 0, 0]]

MaxSubSquare(arr1)

Output:

Complexity Analysis

Time Complexity : O(m*n). This is so because we have to traverse the entire matrix of size m*n. Space Complexity : O(m*n). This is so because we have to store the matrix.

Approach 2 - DP (Top Down)

Consider a matrix with all 0s and 1s. The task is to find the largest square submatrix which would be the largest matrix, and this submatrix should contain all 1s. To understand this approach for finding the maximum size square sub-matrices, let us consider the below matrix to explain the DP (top-down) approach:

The top-left corner should at least have size (n-1)x(n-1) so that an (n x n) sub-matrix can be formed.

Algorithm:

1. Initialize the matrix with values.
2. Call the SubSquare function with suitable parameters.
3. Find the largest square matrix at every row and store it in a variable.
4. Find the largest square matrix at every column and store it in a variable.
5. Now, print the largest value of the square sub-matrix.

• Python Code

def SubSquare(arr1, row, column, max_value):
    # Termination condition
    if row == 0 or column == 0:.

 
        if max_value != 0:
            return arr1[row][column], max(max_value, arr1[row][column])
 
        for i in range(row+1):
                if arr1[i][column] == 1:
                    return 1, 1
 
        for j in range(column+1):
                if arr1[row][j] == 1:
                    return 1, 1
 
        return 0, 0
 
    #finding largestsquare matrix at the specific row
    l, max_value = SubSquare(arr1,row,column-1,max_value)
 
    #finding largestsquare matrix at the specific column
    t, max_value = SubSquare(arr1,row-1,column,max_value)
 
    # Finding largest value of square matrix 
    diagonal, max_value = SubSquare(arr1,row-1,column-1,max_value)
    
    size = 1 + min(min(t,l),diagonal) if arr1[row][column] else 0
 
    
    return size, max(max_value, size)
if __name__ == '__main__':
    arr1 = [
           [0,1,1,1,1,0],
           [1,1,1,1,1,1],
           [0,1,1,1,1,0],
           [0,1,1,1,1,0],
           [1,1,0,1,1,0],
           [1,1,0,1,1,0],
        ]
 
    max_value = SubSquare(arr1, len(arr1) - 1, len(arr1[0]) - 1, 0)[1]
    print("Size of largest square submatrix :", max_value)

Output:

• Java Code

import java.util.concurrent.atomic.AtomicInteger;
class Main
{
    //Finding size of largest square sub matrix
    public static int SubSquare(int[][] arr1, int row, int column, AtomicInteger max_size)
    {
        int i,j;
        // termination condition
        if (row==0||column==0)
        {
            if (max_size.get() != 0)
            {
                max_size.set(Integer.max(max_size.get(), arr1[row][column]));
                return arr1[row][column];
            }
            for(i=0;i<=row;i++)
            {
                if(arr1[i][column] == 1)
                {
                    max_size.set(1);
                    break;
                }
            }
            for (j = 0; j <= column; j++)
            {
                if (arr1[row][j] == 1)
                {
                    max_size.set(1);
                    break;
                }
            }
            return max_size.get();
        }
 

        //Finding largest square matrix at ROW
        int l = SubSquare(arr1,row,column-1,max_size);
 
        //Finding largest square matrix at column
        int t = SubSquare(arr1,row-1,column,max_size);
 
        //Finding largest square matrix in Matrix 
        int d = SubSquare(arr1,row-1,column-1,max_size);
 
        //1+min(three values of largest square matrix)
 
        int size = 0;
        if (arr1[row][column] != 0) {
            size = 1 + Integer.min(Integer.min(t,l),d);
        }
 
        // Maximum size
        max_size.set(Integer.max(max_size.get(), size));
 
        return size;
    }
 
    public static void main(String[] args)
    {
        int[][] arr1 =
        {
                                {0,1,1,1,1,0},
                                {1,1,1,1,1,1},
                                {0,1,1,1,1,0},
                                {0,1,1,1,1,0},
                                {1,1,0,1,1,0},
                                {0,0,1,1,0,0},
        };
        AtomicInteger max_size = new AtomicInteger();
        SubSquare(arr1,arr1.length-1,arr1[0].length-1,max_size);
        System.out.print("Size of largest square submatrix :" +max_size.get());
    }
}

Output:

• C++ code

#include <iostream>
using namespace std;

#define row 6
#define column 7
int SubSquare(int arr1[row][column], int m, int n, int &max_size)
{
    int l,t,tl;
    // base condition
    if (m==0 || n==0)
    {
        if(max_size != 0)
        {
            max_size = max(max_size, arr1[m][n]);
            return arr1[m][n];
        }
 
        for (int i = 0; i <= m; i++)
        {
            if (arr1[i][n] == 1)
            {
                max_size = 1;
                break;
            }
        }
 
        for (int j = 0; j <= n; j++)
        {
            if (arr1[m][j] == 1)
            {
                max_size = 1;
                break;
            }
        }
 
        return max_size;
    }
 
    // Finding largest square matrix at row
    l = SubSquare(arr1, m, n - 1, max_size);
 
    // Finding largest square matrix at column
    t = SubSquare(arr1, m - 1, n, max_size);
 
    // Finding largest square matrix of matrix
    tl = SubSquare(arr1, m - 1, n - 1, max_size);
 
            // Maximum size
            //max_size.set(Integer.max(max_size.get(), size))
    int size = 0;
    if (arr1[m][n] != 0) {
        size = 1 + min (min(t, l), tl);
    }
 
    max_size = max(max_size, size);

    return size;
}
 
int main()
{
    int arr1[row][column] =
    {
                                {0,1,1,1,1,0},
                                {1,1,1,1,1,1},
                                {0,1,1,1,1,0},
                                {0,1,1,1,1,0},
                                {1,1,0,1,1,0},
                                {0,0,1,1,0,0},
    };
     int size = 0;
    
    SubSquare(arr1, row - 1, column - 1, size);
 
    cout << "Size of largest square sub matrix is: " << size;
 
    return 0;
}

Output:

Conclusion

In this tutorial, we have discussed the problem “Maximum size square submatrix with all 1s” with an in-depth explanation of its solution. We started with a general introduction of the problem statement with an example and then we discussed two dynamic programming approaches to solve the problem.

We certainly hope that by going through this article, you will be able to understand how to solve the problem of maximum size square sub-matrices with all 1s with ease.

People are also reading:

• Union vs Structure
• DSA – Greedy Algorithms
• Python Data Structure
• Algorithms Basics
• Matrix Multiplication in C
• Tree vs Graph
• Array vs List
• Linked List
• Python List or Array
• What is Stack in Data?