Check if directed graph is connected

Problem

Given a directed graph, check if it is connected or not.

Sample Input

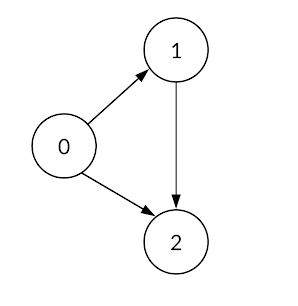
Sample Output

YES

Explanation

Start from 0, go to 1, and then 2; hence all the nodes of the graph are connected.

Approach

We will use the Depth First Search algorithm to solve this problem. We will traverse the given graph and keep marking nodes as visited, and check the required conditions to check the connected component. Below is the algorithm to solve this problem:

1. Consider two boolean arrays, vis1 and vis2, both of which are set to false.
2. Begin with a random vertex in the graph and perform a Depth First Search.
3. Make the current visited node vis1[v] = true.
4. All of the edges should now be reversed in the direction.
5. Begin Depth First Search at the vertex selected in step 2.
6. Make the current visited node vis2[v] = true.
7. The graph is not connected if any vertex v has vis1[v] = false and vis2[v] = false.

C++ Programming

#include <bits/stdc++.h>
using namespace std;
#define N 100000

vector<int> adj1[N], adj2[N];

bool vis1[N], vis2[N];

void dfs1(int node)
{
    vis1[node] = true;

    for (auto i : adj1[node])
        if (!vis1[i])
            dfs1(i);
}

void dfs2(int node)
{
    vis2[node] = true;

    for (auto i : adj2[node])
        if (!vis2[i])
            dfs2(i);
}

bool solve(int n)
{
    memset(vis1, false, sizeof vis1);
    dfs1(1);

    // reverse direction call
    memset(vis2, false, sizeof vis2);
    dfs2(1);

    for (int i = 0; i < n; i++) {
        // If any vertex it not visited in any direction, then graph is not connected
        if (!vis1[i] and !vis2[i])
            return false;
    }
    return true;
}

int main()
{
    int n = 3;

    adj1[0].push_back(1);
    adj2[1].push_back(0);
    adj1[1].push_back(2);
    adj2[2].push_back(1);
    adj1[0].push_back(2);
    adj2[2].push_back(0);


    if (solve(n))
        cout << "YES";
    else
        cout << "NO";

    return 0;
}

Output

YES

Java Programming

import java.util.*;

class Solution
{
    static int N = 1000;

    static Vector<Integer>[] adj1 = new Vector[N];
    static Vector<Integer>[] adj2 = new Vector[N];

    static boolean[] vis1 = new boolean[N];
    static boolean[] vis2 = new boolean[N];

    static {
        for (int i = 0; i < N; i++)
        {
            adj1[i] = new Vector<>();
            adj2[i] = new Vector<>();
        }
    }

    static void MakeGraph(int u, int v)
    {
        adj1[u].add(v);
        adj2[v].add(u);
    }

    static void dfs1(int x)
    {
        vis1[x] = true;
        for (int i : adj1[x])
            if (!vis1[i])
                dfs1(i);
    }

    static void dfs2(int x)
    {
        vis2[x] = true;
        for (int i : adj2[x])
            if (!vis2[i])
                dfs2(i);
    }

    static boolean solve(int n)
    {
        // Call for initial direction
        Arrays.fill(vis1, false);
        dfs1(1);

        // Call for reverse direction
        Arrays.fill(vis2, false);
        dfs2(1);

        for (int i = 1; i <= n; i++)
        {
            // If any vertex it not visited in any direction
            // Then graph is not connected
            if (!vis1[i] && !vis2[i])
                return false;
        }
        return true;
    }

    public static void main(String[] args)
    {
        int n = 3;

        MakeGraph(1, 2);
        MakeGraph(2, 3);
        MakeGraph(1, 3);

        if (solve(n))
            System.out.println("YES");
        else
            System.out.println("NO");
    }
}

Output

YES

Python Programming

N = 1000
adj1 = {}
adj2 = {}

vis1 = [0] * N; vis2 = [0] * N;

def CreateGraph(u, v):
    if u not in adj1 :
        adj1[u] = [];
        
    if v not in adj2 :
        adj2[v] = [];
        
    adj1[u].append(v);
    adj2[v].append(u);

def dfs1(node) :
    vis1[node] = True;
    if node not in adj1 :
        adj1[node] = {};
        
    for i in adj1[node] :
        if (not vis1[i]) :
            dfs1(i)

def dfs2(node) :
    vis2[node] = True;

    if node not in adj2 :
        adj2[node] = {};
        
    for i in adj2[node] :
        if (not vis2[i]) :
            dfs2(i);

def solve(n) :

    global vis1;
    global vis2;
    # Call for correct direction
    vis1 = [False] * len(vis1);
    dfs1(1);
    
    # Call for reverse direction
    vis2 = [False] * len(vis2);
    dfs2(1);
   
    for i in range(1, n + 1) :
        # If any vertex it not visited in any direction
        # Then graph is not connected
        if (not vis1[i] and not vis2[i]) :
            return False;            
    return True;

if __name__ == "__main__" :
    n = 3;

    CreateGraph(1, 2);
    CreateGraph(2, 3);
    CreateGraph(1, 3);
    
    if (solve(n)) :
        print("Yes");

    else :
        print("No");

Output

YES

People are also reading:

• Find dropping point of an egg
• Print all subarrays of an array having distinct elements
• Count Inversions
• Hybrid QuickSort Algorithm
• Quicksort algorithm using Hoare’s partitioning scheme
• Create a mirror of an m–ary Tree
• Construction of an Expression Tree
• Dutch National Flag Problem
• Subarray with Sum k
• Maximum Sum Circular Subarray