Insertion Sort in C

Before explaining the insertion sort in c, you must know what is sorting and why to use it. In simple words, sorting is a way to arrange any collection of data in a systematic or orderly manner that can be either numbers or alphabets. The need for sorting becomes very high when the amount of data is large. Sorting techniques arranges data for different purposes in large organizations.

Algorithms or techniques sorting data in ascending or descending order are sorting algorithms and are a part of the data structures. There are various types of sorting algorithms in the data structure and used for different needs and requirements. In this article, we will see the working of Insertion Sort. Let’s start it with understanding the basics of insertion sort.

What is Insertion Sort?

A set of playing cards is the best example to explain the insertion sort algorithm. Insertion sort is an in-place comparison-based algorithm in which the input element is compared with all the rest of the elements that are in the list and placed to the correct position to which it belongs in the sorted list. Insertion sort can be used for sorting both lists and arrays. It is a straightforward algorithm with the time complexity of O(n^2).

Algorithm

The algorithm consists of following steps: 1: arr[n], n is the size of the array 2: insertionSort(arr,n) 3: Loop from i=1 to n-1 4: Pick element arr[i] and insert it into sorted arr[0…i-1] To understand this in more practical, let’s take an example- In the below example, we have the size of the array n as 8, starting from the first element, each element is compared with the other elements and placing it in the right sequence. Input Array: 4, 3, 2, 10, 12, 1, 5, 6 Insertion Sort in C

Output- a sorted sequenced array: 1, 2, 3, 4, 5, 6, 10, 12

Example of Insertion Sort using C Programming

// Insertion sort using C program
#include <stdio.h>
#include <math.h>
/* Function that is used in insertion sort to sort an array */
void insertionSort(int arr[], int n) 
{ 
int i, key, j; 
for (i = 1; i < n; i++) 
{ 
key = arr[i]; 
j = i-1; 
/* Move elements of arr[0..i-1], if it is greater than key, to one position ahead of their current position */
while (j >= 0 && arr[j] > key) 
{ 
arr[j+1] = arr[j]; 
j = j-1; 
} 
arr[j+1] = key; 
} 
} 
// The utility function to print an array of size n 
void printArray(int arr[], int n) 
{ 
int i; 
for (i=0; i < n; i++) 
printf("%d ", arr[i]); 
printf("\n"); 
} 
/* Driver program to test insertion sort */
int main() 
{ 
int arr[] = {12, 11, 13, 5, 6}; 
int n = sizeof(arr)/sizeof(arr[0]); 
insertionSort(arr, n); 
printArray(arr, n); 
return 0; 
}

Explanation-

22 , 3, 19, 5, 11, 34 Let us loop for i = 1 (second element of the array) to 6 (Size of input array) i = 1. Since 3 is smaller than 22, move 22 and insert 3 before 22 3, 22 , 19, 5, 11, 34 i = 2. Since 19 smaller than 22, move 22 and insert 19 before 22. 3, 19, 22 , 5, 11, 34 i = 3. 5 will move to after 3, and all other elements from 19 to 34 will move one position ahead of their current position. 3, 5, 19, 22, 11, 34 i = 4. 11 will move to the third position after 5, and all other elements from 19 to 34 will move one position ahead of their current position. 3, 5, 11, 19, 22, 34 i = 5. 34 will remain at its position as all elements in A[0..I-1] are smaller than 34 3, 5, 11, 19, 22, 34 Output: 5, 6, 11, 12 13

Example of Insertion Sort using Java

public class InsertionSort
{  
    public static void insertionSort(int array[]) 
{  
        int n = array.length;  
        for (int j = 1; j < n; j++) {  
            int key = array[j];  
            int i = j-1;  
            while ( (i > -1) && ( array [i] > key ) ) {  
                array [i+1] = array [i];  
                i--;  
            }  
            array[i+1] = key;  
        }  
    }  
   public static void main(String a[]){    
        int[] arr1 = {22, 3, 19, 5, 11, 34};    
        System.out.println("Before Insertion Sort");    
        for(int i:arr1){    
            System.out.print(i+" ");    
        }    
        System.out.println();                
        insertionSort(arr1);//sorting array using insertion sort               
        System.out.println("After Insertion Sort");    
        for(int i:arr1){    
            System.out.print(i+" ");    
        }    
    }    
}    
>

Output:

Before Insertion Sort

22 3 19 5 11 34

After Insertion Sort

3 5 11 19 22 34

Example of Insertion Sort using C++

#include<bits/stdc++.h>
using namespace std;

void applyInsertion(int arr[], int n)
{
	int i, keyElement, j;
	for (i = 1; i < n; i++) 
        { 
               keyElement = arr[i]; 
               j = i - 1; 

                while (j >= 0 && arr[j] > keyElement) 
                {
			arr[j + 1] = arr[j];
			j = j - 1;
		}
		arr[j + 1] = keyElement;
	}
}

int main()
{
	int arr[] = { 1, 2, 4, 3 };
	int n = sizeof(arr) / sizeof(arr[0]);

	applyInsertion(arr, n);
	for (int i = 0; i < n; i++)
		cout<<arr[i]<<" ";

	return 0;
}

Output

1 2 3 4

Example of Insertion Sort using Python

def applyInsertion(arr):

	for i in range(1, len(arr)):

		keyElement = arr[i]

		j = i-1
		while j >= 0 and keyElement < arr[j] :
				arr[j + 1] = arr[j]
				j -= 1
		arr[j + 1] = keyElement


arr = [1, 2, 4, 3]
applyInsertion(arr)
for i in range(len(arr)):
	print (arr[i],end=" ")

Output

1 2 3 4

Real-Time Application

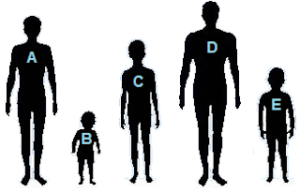
Insertion sort works on a compassion-based technique by shifting and putting the elements in its correct position. If five persons are in a queue and all are of different heights. If they are to be arranged in order of their heights i.e, shortest to tallest then it can be done using insertion sorts. Example 1

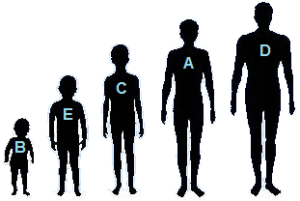
The image above shows people with different heights. After comparing person B with person A, person A is shifted to the place of person B as person B is smaller than person A. Similarly on comparing persons A and C, person takes the position of person A as C is shorter to person A. This process is repeated until we get all of them standing in their heights shortest to tallest order that is: Person B, Person E, Person C, Person A, Person D The image below shows the sorted arrangement of the person from the shortest to the tallest.

Insertion Sort

Advantages

Insertion sort can be implemented simply than other quadratic sorting algorithms .
It is a stable algorithm, which means it does not change the sequence of the elements which have equal keys.
It is the in-place algorithm as it does not require additional memory space.
Efficient and adaptive for substantially sorted data sets.
Insertion sort is the most efficient in practice than selection sort or bubble sort .
It is important to tell you that insertion sort is online that it can sort a list as it receives it.

Disadvantages

It is slow for unsorted or reverses sorted data.
The algorithm is not efficient for large data collection.
It requires a large number of data shifts.
The worst-case complexity is of O(n^2) as it compares each element with the whole list, this takes more time.
The performance is low.

People are also reading:

Insertion Sort [Algorithm & Program]

Table of Content